Mate
Para razonar y comprender
Categoría: Geometría Euclidiana
-

Los axiomas formalizan la noción de «estar entre», permitiendo definir conceptos como segmento, rayo, y polígonos, así como establecer propiedades de ordenamiento geométrico. Relación primitiva: «Entre» En la geometría de Hilbert, los axiomas de orden se basan en una única relación primitiva implícita: la relación ternaria «estar entre» (betweenness en inglés), denotada como A-B-C (que significa «el punto B…
-
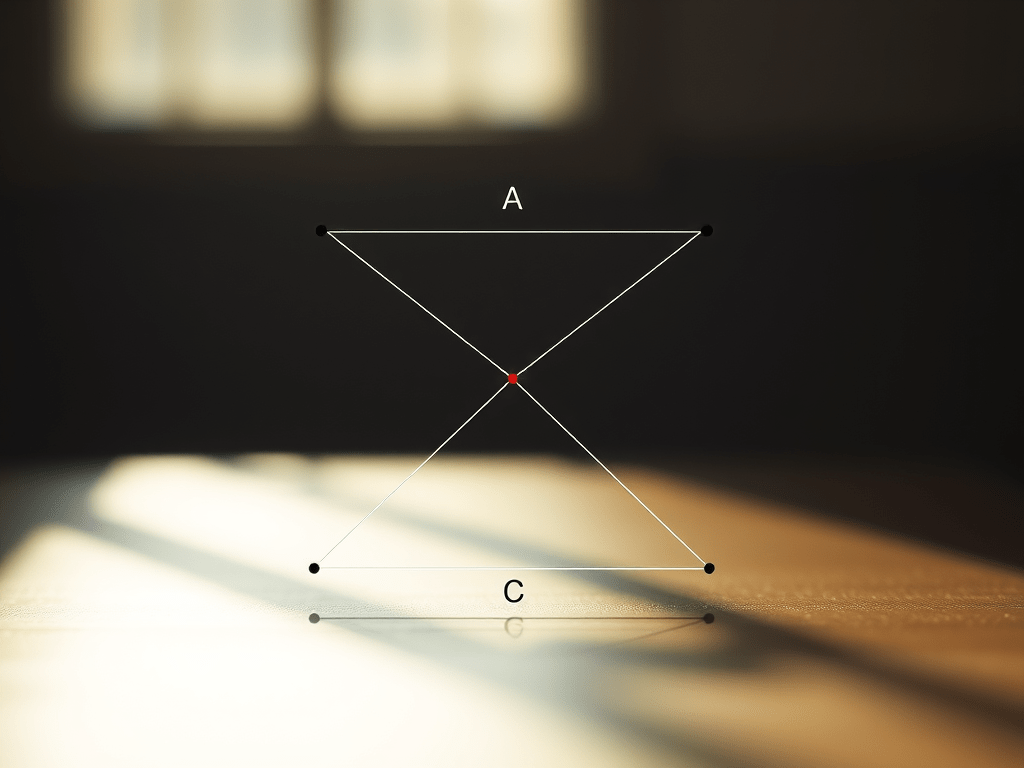
Los axiomas formalizan la noción de «estar entre», permitiendo definir conceptos como segmento, rayo, y polígonos, así como establecer propiedades de ordenamiento geométrico. Relación primitiva: «Entre» Axioma II1 (Propiedad Simétrica) Axioma II2 (Existencia de un punto intermedio) Axioma II3 (Extensión de la recta) Axioma II4 (Unicidad del orden) Axioma II5 (Axioma de Pasch)
-

Teorema «Dos rectas secantes determinan un único plano al cual pertenecen.» Gráfico. Demostración ? Tarea Te animas a completar la hipótesis, la tesis y la demostración, más algún gráfico de ayuda. Ver como ayuda Teorema 1 y Teorema 2.
-

Teorema «Una recta y un punto exterior a ella determinan un único plano al cual pertenecen.» Demostración Por el axioma I2 sabemos que la recta r tiene a lo sumo dos puntos, llamémoslos Q y R. Como P no pertenece a la recta, por definición, tenemos tres puntos no alineados. Por el axioma I4, los…
-

Teorema «Si dos rectas distintas tienen a lo sumo un único punto en común.» Demostración Vamos a realizar la demostración por reducción al absurdo. Supongamos que no tenemos un único punto de intersección, tenemos dos puntos. Por el Axioma I1 dos puntos determinan una única recta y como P y Q pertenecen a r y…
-

Rectas Secantes (que se intersecan)
-
Definición Dos rectas r y s son paralelas (r ∥ s) si y solo si: Observación:
-

En la geometría axiomática de Hilbert, los axiomas de incidencia (enlace o conexión) no solo se basan en conceptos primitivos no definidos (punto, recta, plano), sino también en relaciones primitivas implícitas que conectan estos conceptos. Estas relaciones no se definen formalmente, pero su significado se deduce de cómo se usan en los axiomas. Aquí están…
-

Relaciones entre Puntos y Rectas Estos axiomas describen cómo los puntos y las rectas interactúan: Axioma I1 (Unicidad de la recta): Dados dos puntos distintos A y B, existe una única recta r que pasa por ambos. Axioma I2 (Existencia mínima): Toda recta contiene al menos dos puntos. Axioma I3 (Espacio Bidimensional): Dada una recta existe al menos un punto que no…
-

¿Qué es la Geometría Euclidiana? La geometría euclidiana es el sistema geométrico basado en los postulados introducidos por Euclides en su obra Elementos (siglo III a.C.). Es la geometría clásica que estudia las propiedades del plano y el espacio tridimensional, donde valen axiomas como el de las paralelas y la congruencia de figuras. Características Fundamentales…




