Mate

---

Definición: Dos triángulos son semejantes si tienen sus ángulos correspondientes iguales y sus lados proporcionales. Esto implica que tienen la misma forma pero no necesariamente el mismo tamaño.

Notación:
Si △ ABC ∼△ DEF, entonces:

• ∠A = ∠D, ∠B = ∠E, ∠C = ∠F.
• 
  (razón de semejanza).

---

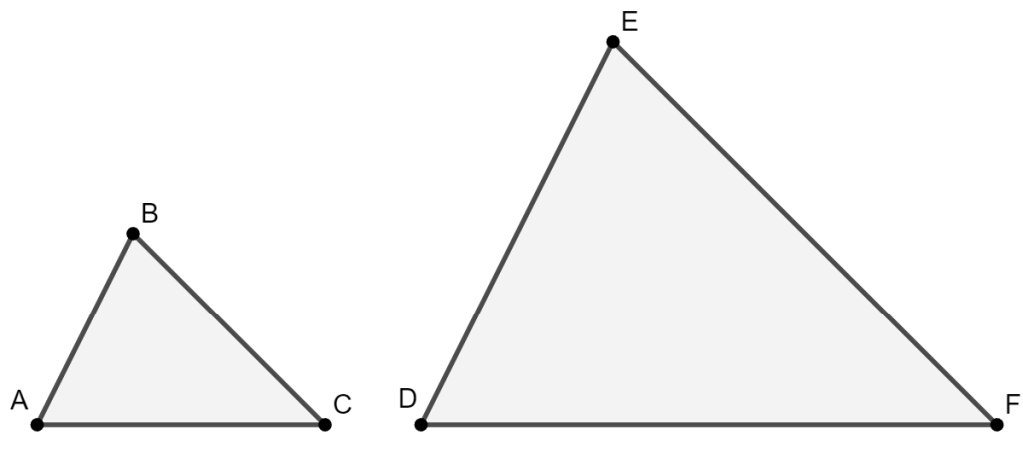
Criterios de Semejanza de Triángulos

1. Criterio Ángulo-Ángulo (AA o AAA)

• Condición: Dos ángulos correspondientes iguales.
• Ejemplo:
  Si ∠A = ∠D y ∠B = ∠E, entonces △ABC ∼ △DEF.

2. Criterio Lado-Ángulo-Lado (LAL)

• Condición: Un ángulo igual y los lados que lo forman son proporcionales.
• Ejemplo:
  Si ∠A = ∠D y AB/DE = AC/DF, entonces △ABC ∼ △DEF.

3. Criterio Lado-Lado-Lado (LLL)

• Condición: Los tres lados son proporcionales.
• Ejemplo:
  Si AB/DE = BC/EF = AC/DF, entonces △ABC ∼ △DEF.

---

Criterios de Semejanza para Triángulos Rectángulos

En triángulos rectángulos, además de los criterios generales, existen dos criterios adicionales debido a que tienen un ángulo recto ((90°)) común.

1. Criterio Cateto-Cateto (CC)

• Condición: Los dos catetos son proporcionales.
• Ejemplo:
  Si AB/DE = BC/EF donde AB y BC son catetos, entonces △ABC ∼ △DEF.

2. Criterio Hipotenusa-Cateto (HC)

• Condición: La hipotenusa y un cateto son proporcionales.
• Ejemplo:
  Si AB/DE = BC/EF (donde AC y DF son hipotenusas), entonces △ABC ∼ △DEF.

---

Ejemplo Práctico

Problema:
Demuestra que los triángulos rectángulos (\triangle ABC) y (\triangle DEF) son semejantes si:

• ∠ B = ∠ E = 90°,
• AB = 3, BC = 4, DE = 6, EF = 8.

Solución:

1. Aplicamos el criterio Cateto-Cateto (CC):
   
   Como la razón es igual, △ABC ∼ △DEF.

---

Aplicaciones de la Semejanza de Triángulos

• Medición indirecta de alturas (como árboles o edificios usando sombras).
• Diseño de escalas (maquetas, mapas).
• Óptica (lentes, espejos).

Dato clave: En triángulos rectángulos, la altura sobre la hipotenusa genera dos triángulos semejantes entre sí y al original.

---

Resumen Visual

Criterio General	Triángulos Rectángulos
AA (2 ángulos iguales)	CC (Catetos proporcionales)
LAL (lado-ángulo-lado)	HC (Hipotenusa-cateto)
LLL (3 lados proporcionales)	También aplica AA

---