Mate
Para razonar y comprender
Categoría: Geometría
-

Relaciones entre Puntos y Rectas Estos axiomas describen cómo los puntos y las rectas interactúan: Axioma I1 (Unicidad de la recta): Dados dos puntos distintos A y B, existe una única recta r que pasa por ambos. Axioma I2 (Existencia mínima): Toda recta contiene al menos dos puntos. Axioma I3 (Espacio Bidimensional): Dada una recta existe al menos un punto que no…
-

En un sistema de coordenadas en la recta (o sistema unidimensional), cada punto sobre una línea recta queda determinado por un único número real llamado abscisa (o coordenada ). Veamos en qué consiste: Elementos Básicos Recta numérica (eje ): Abscisa (): Propiedades Clave Correspondencia biunívoca: Orden: Operaciones y Aplicaciones a) Distancia entre dos puntos b)…
-

¿Qué es la Geometría Euclidiana? La geometría euclidiana es el sistema geométrico basado en los postulados introducidos por Euclides en su obra Elementos (siglo III a.C.). Es la geometría clásica que estudia las propiedades del plano y el espacio tridimensional, donde valen axiomas como el de las paralelas y la congruencia de figuras. Características Fundamentales…
-

La Geometría como Sistema Axiomático La geometría, en su enfoque moderno, es un sistema axiomático formal que organiza el conocimiento matemático a partir de conceptos primitivos, definiciones, axiomas y teoremas. A continuación, se detallan sus características y elementos clave, siguiendo el modelo establecido por David Hilbert en Fundamentos de la Geometría (1899). Características Principales Rigor…
-
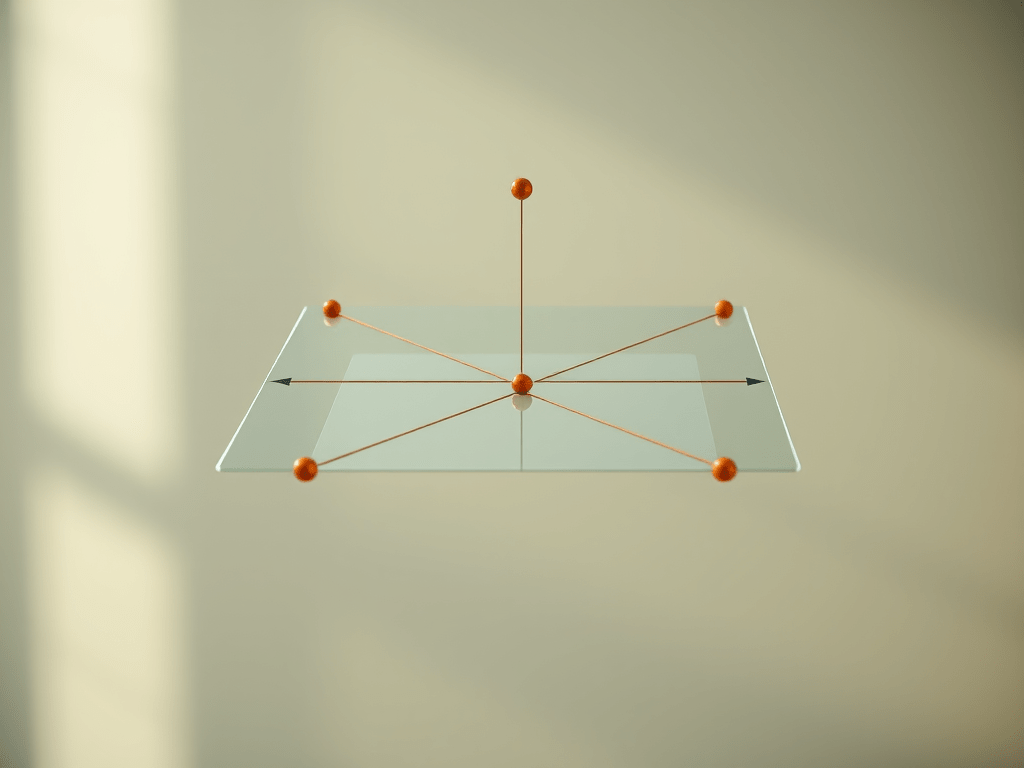
Definición de Puntos Coplanares En geometría, los puntos coplanares son un conjunto de puntos que pertenecen al mismo plano. Es decir, existe un plano (superficie bidimensional infinita) que contiene a todos ellos. Explicación Detallada Cómo Determinar si Puntos son Coplanares Método geométrico (para 4 puntos): Verifica si 3 puntos son colineales: Si no son colineales:…
-

Definición de Puntos Alineados En la geometría de Hilbert, la alineación de puntos se define estrictamente a partir de los axiomas de incidencia y el concepto primitivo de recta. Aquí está la formalización rigurosa: Definición Formal Un conjunto de puntos se dice alineado (o colineal) si existe una recta tal que todos los puntos pertenecen…
-

Los axiomas de incidencia en la geometría de Hilbert establecen las relaciones fundamentales entre los conceptos primitivos (punto, recta y plano), sin depender de nociones como distancia o ángulos. Estos axiomas definen cómo estos objetos se conectan entre sí y garantizan la existencia de una estructura geométrica mínima. A continuación, se presenta su significado y…
-

El Plano es un Concepto Primitivo en Geometría Euclidiana En la geometría clásica de Euclides, el plano es el tercer concepto primitivo fundamental, junto con el punto y la recta. Euclides lo define en el Libro I, Definición 5 como: «Una superficie es aquello que solo tiene longitud y anchura»,y más adelante especifica que un…
-

La Recta es un Concepto Primitivo en Geometría Euclidiana En la geometría euclidiana, la recta (o línea recta) es otro concepto primitivo, al igual que el punto y el plano. Euclides la introduce en el Libro I, Definición 2 de Los Elementos con la frase: «Una línea es una longitud sin anchura» (en griego: γραμμὴ…
-

El Punto es un Concepto Primitivo en Geometría Euclidiana En la geometría de Euclides (expuesta en Los Elementos, siglo III a.C.), el punto es uno de los conceptos fundamentales e indefinidos, es decir, no se explica en términos más básicos, sino que se asume como una noción intuitiva a partir de la cual se construyen…




