Mate
Para razonar y comprender
Categoría: Geometría
-

Definición Un triángulo △ABC se llama isósceles si tiene al menos dos lados congruentes. Por ejemplo: Elementos clave: Base en los Axiomas de Hilbert Congruencia de segmentos (Axioma III.1-III3): Congruencia de ángulos (Axioma III.4-III.6): Propiedades Inmediatas Simetría: Equivalencia: Teorema Relacionado (Por Demostrar Más Adelante) Teorema del Triángulo Isósceles:En un triángulo isósceles, los ángulos opuestos a…
-
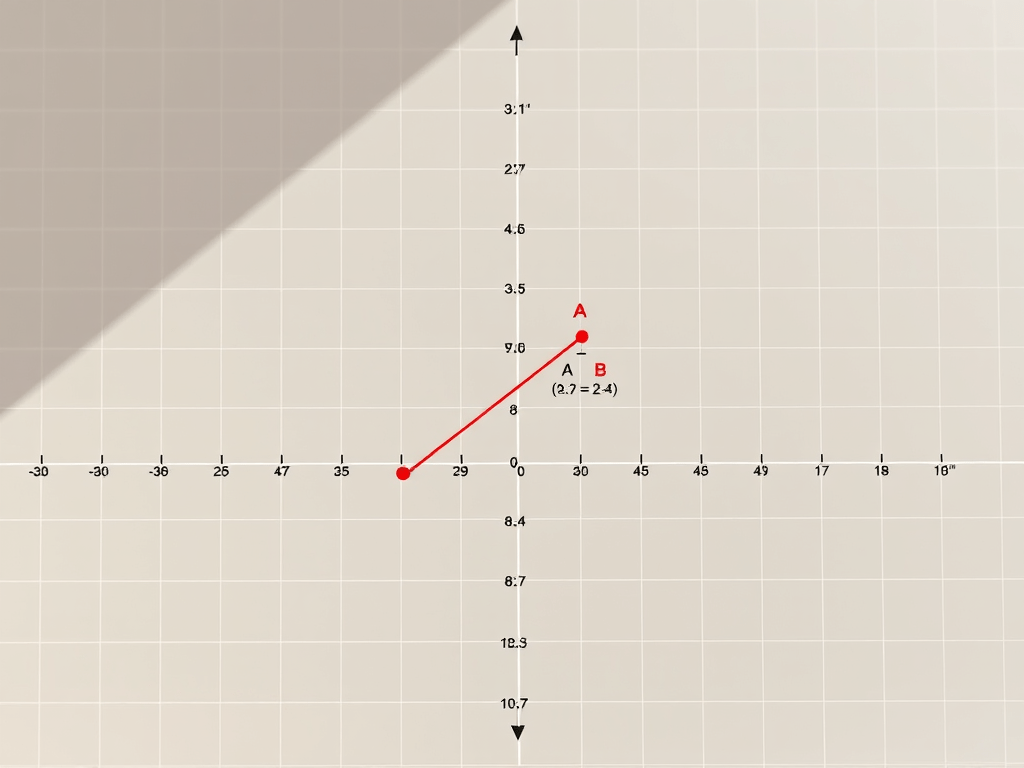
Fórmula de Distancia entre Dos Puntos en el Plano (2D) Dados dos puntos en el plano cartesiano: La distancia euclidiana ( d(A, B) ) entre ellos se calcula con: Explicación Base en el Teorema de Pitágoras: Pasos para derivar la fórmula: Ejemplo Práctico Puntos: Diferencias: Cuadrados: Distancia: Casos Especiales Puntos sobre una recta horizontal: Puntos…
-

Congruencia de Triángulos En Geometría, la congruencia de triángulos se define mediante la congruencia de sus lados y ángulos correspondientes, utilizando los axiomas de congruencia (III1-III7). Aquí está la construcción rigurosa: Definición Formal Dos triángulos △ABC y △A’B’C’ son congruentes si y solo si se cumplen las siguientes seis condiciones: Lados correspondientes congruentes: Ángulos correspondientes…
-

Definición de Triángulo en la Geometría Un triángulo es una figura geométrica básica construida a partir de segmentos y puntos no alineados. Aquí está su definición formal y propiedades derivadas: Definición Formal Dados tres puntos no alineados A, B, y C, el triángulo △ ABC es la unión de los tres segmentos que los conectan:…
-

Congruencia de Segmentos Axioma III.1 (Transporte de un segmento) Dado un segmento AB y un punto A’ origen de una semirrecta s, existe un punto B’ en la semirrecta de tal manera que: Axioma III.2 La congruencia de segmentos es una relación de equivalencia. Propiedad reflexiva: todo segmento es congruente consigo mismo. Propiedad simétrica: si…
-

Un ángulo se define como una figura geométrica específica formada por la unión de dos semirrectas (o rayos) que comparten un origen común pero no son colineales. Aquí presentamos la definición rigurosa, sus componentes clave y su base en los axiomas: Definición Formal Dados tres puntos no alineados A, O, B, el ángulo ∠AOB es…
-

En el sistema axiomático de Hilbert, un semiplano es una de las dos regiones convexas en las que una recta divide a un plano. Su definición precisa se basa en los axiomas de orden y el Teorema de Separación del Plano. Aquí está la construcción rigurosa. Definición Formal Dada una recta r en un plano…
-

En el sistema axiomático de Hilbert, una semirrecta se define a partir de los axiomas de orden y el concepto primitivo «estar entre» (A-B-C). Definición Formal Dados dos puntos distintos O (origen) y A, la semirrecta de origen O que pasa por A es el conjunto de puntos formado por: En símbolos: Base en los…
-

Las geometrías no euclidianas son sistemas geométricos que no cumplen uno o más de los postulados clásicos de la geometría euclidiana (basada en los Elementos de Euclides, siglo III a.C.). Surgen al cuestionar el quinto postulado de Euclides (el postulado de las paralelas), lo que llevó a descubrir espacios con curvatura, donde las reglas familiares…
-

Las razones trigonométricas relacionan los ángulos agudos de un triángulo rectángulo con las proporciones entre sus lados. Se definen para un ángulo θ (distinto del ángulo recto) de la siguiente manera: Definiciones Básicas Dado un triángulo rectángulo con: Las 6 razones trigonométricas principales son: Razón Definición Fórmula Seno (sen) Cateto opuesto / Hipotenusa Coseno (cos)…




