Función Lineal: Definición y Análisis
1. Definición
Una función lineal es una función polinómica de primer grado de la forma:
- m y b son constantes reales (m, b ∈ R).
- x es la variable independiente.
Dominio y codominio:
- Por defecto,
(está definida para todos los números reales).
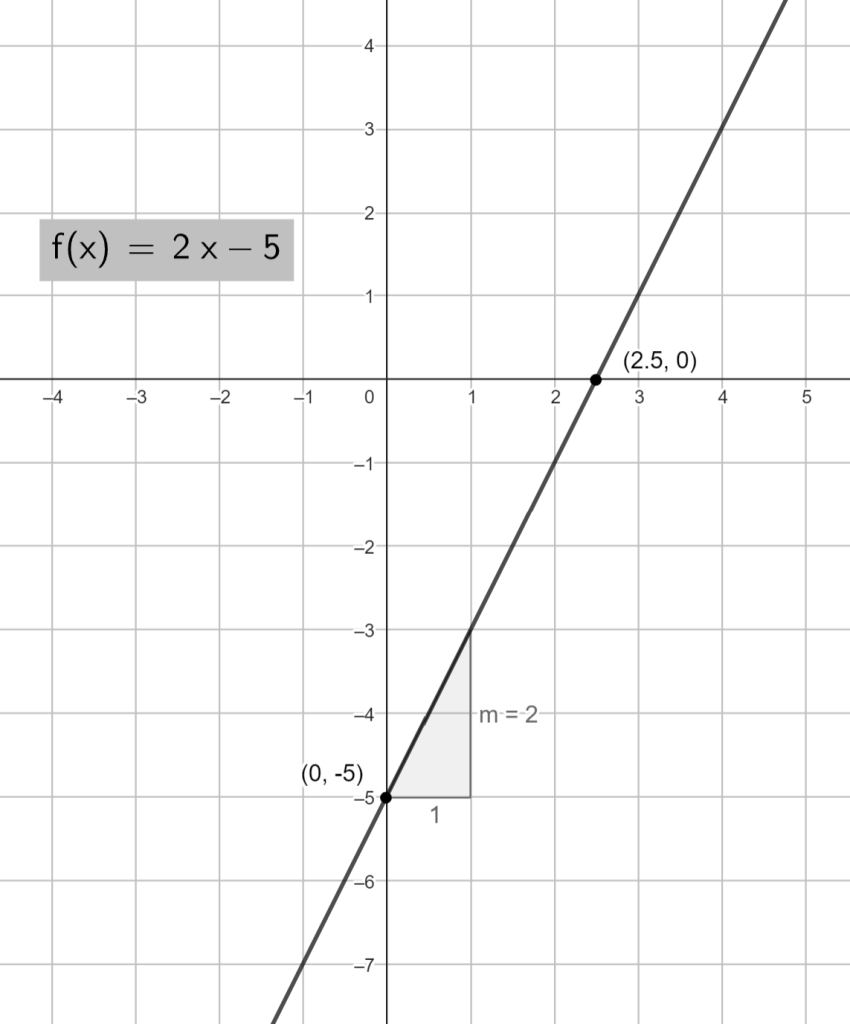
2. Gráfica de la función lineal
La gráfica de una función lineal es una recta en el plano cartesiano.
Características clave:
- Intersección con el eje y (ordenada al origen): Punto (0, b).
- Pendiente (m): Determina la inclinación y dirección de la recta (ver punto 4).
3. Análisis de los parámetros
- Pendiente ( m ):
- Si m > 0: La recta es creciente.
- Si m < 0: La recta es decreciente.
- Si m = 0: La función es constante (f(x) = b).
- Ordenada al origen ( b ):
- Indica dónde la recta corta al eje y.
- Si (b = 0), la recta pasa por el origen (0, 0) (función lineal homogénea).
4. Pendiente de la recta (definición analítica)
La pendiente m se define como la razón de cambio de la función:
para cualquier par de puntos en la recta.
Interpretación:
- m cuantifica cuánto aumenta (o disminuye) f(x) por cada unidad que aumenta x.
5. Raíces (ceros de la función)
La raíz de la función lineal es el valor de x que anula la función, es decir, donde f(x)=0:
- Geométricamente: Es la abscisa del punto donde la recta corta al eje x.
- Función constante: Si
, la función no tiene raíces (recta horizontal paralela al eje x).
- Si m = 0 y b = 0, todos los x son raíces (recta y = 0).
6. Ejemplo práctico
Dada f(x) = 2x – 4:
- Pendiente: m = 2 (recta creciente).
- Ordenada al origen: b = -4 (corta al eje y en (0, -4)).
- Raíz:






Deja un comentario