Axiomas de Congruencia

Congruencia de Segmentos

Axioma III.1 (Transporte de un segmento)

Dado un segmento AB y un punto A’ origen de una semirrecta s, existe un punto B’ en la semirrecta de tal manera que:

$\overline{AB} \cong \overline{A'B?}$

Axioma III.2

La congruencia de segmentos es una relación de equivalencia.

Propiedad reflexiva: todo segmento es congruente consigo mismo.

$\overline{AB} \cong \overline{AB}$

Propiedad simétrica: si un segmento es congruente con otro, también el segundo es congruente con el primero.

$\overline{AB} \cong \overline{CD} \implies \overline{CD} \cong \overline{AB}$

Propiedad transitiva: si un segmento es congruente con otro y este último con un tercero, entonces el primer segmento es congruente con el tercero.

$\overline{AB} \cong \overline{CD} \text{ y } \overline{CD} \cong \overline{EF}\implies \overline{AB} \cong \overline{EF}$

Axioma III.3

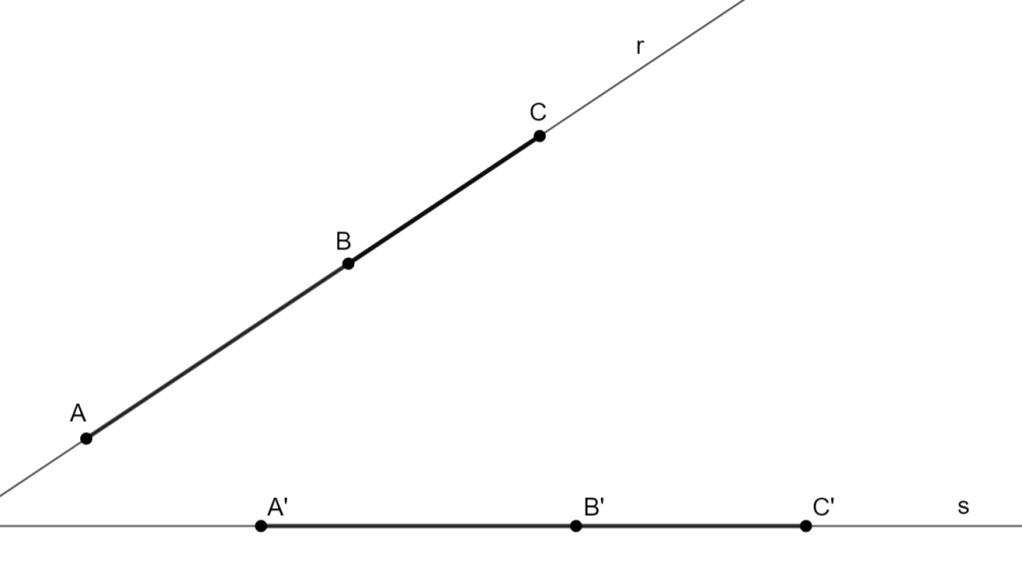
Supongamos que tenemos tres puntos alineados en una recta r:
A – B – C

Supongamos que tenemos tres puntos alineados en una recta s:
A’ – B’ – C’

Si:

$\overline{AB} \cong \overline{A'B'}$

$\overline{BC} \cong \overline{B'C?}$

Entonces:

$\overline{AC} \cong \overline{A'C'}$

Congruencia de Ángulos

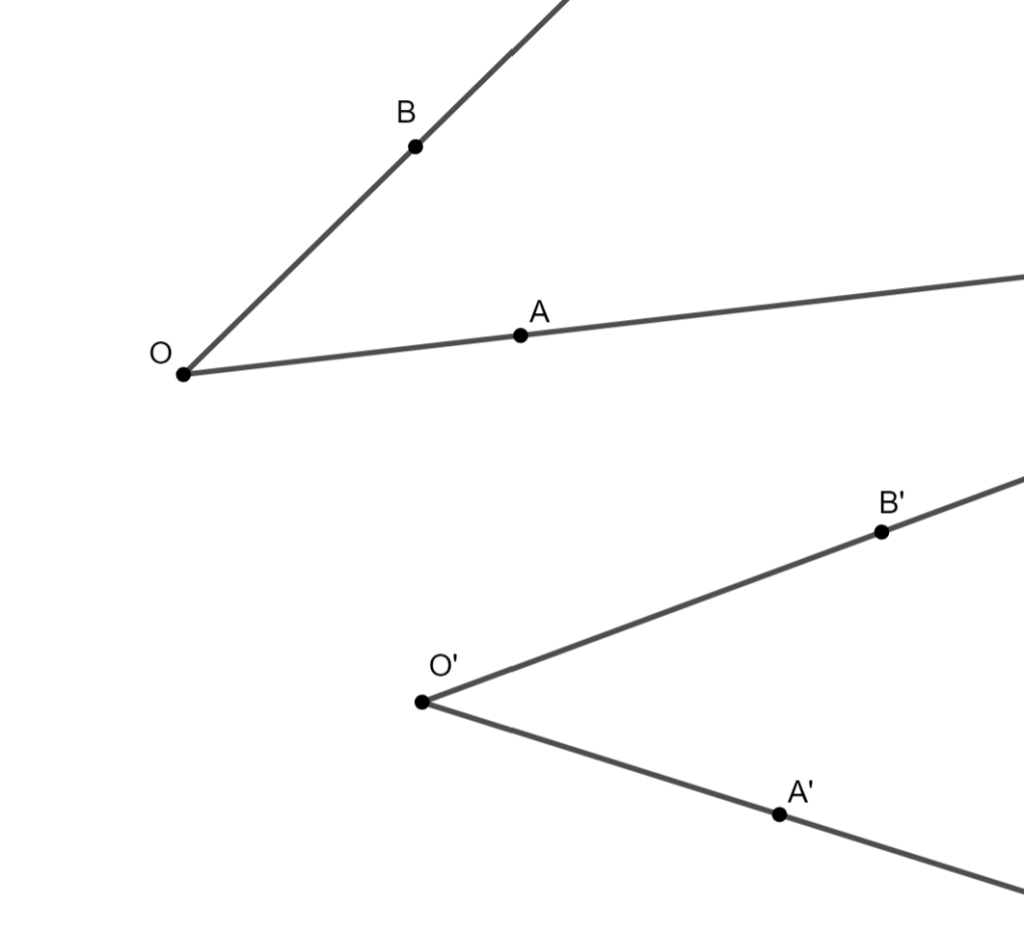
Axioma III.4 (Transporte de un ángulo)

Dado un ángulo ∠ AOB, una semirrecta O′A′, y un semiplano α respecto a O′A′, existe una única semirrecta O′B′ en α tal que:

$\angle AOB \cong \angle A'O'B'$

Axioma III.5 (Equivalencia de ángulos)

La congruencia de ángulos es una relación de equivalencia.

Propiedad reflexiva: todo ángulo es congruente consigo mismo.

$\angle \alpha \cong \angle \alpha$

Propiedad simétrica: si un segmento es congruente con otro, también el segundo es congruente con el primero.

$\angle \alpha \cong \angle \beta\implies \angle \beta\cong \angle \alpha$

Propiedad transitiva: si un segmento es congruente con otro y este último con un tercero, entonces el primer segmento es congruente con el tercero.

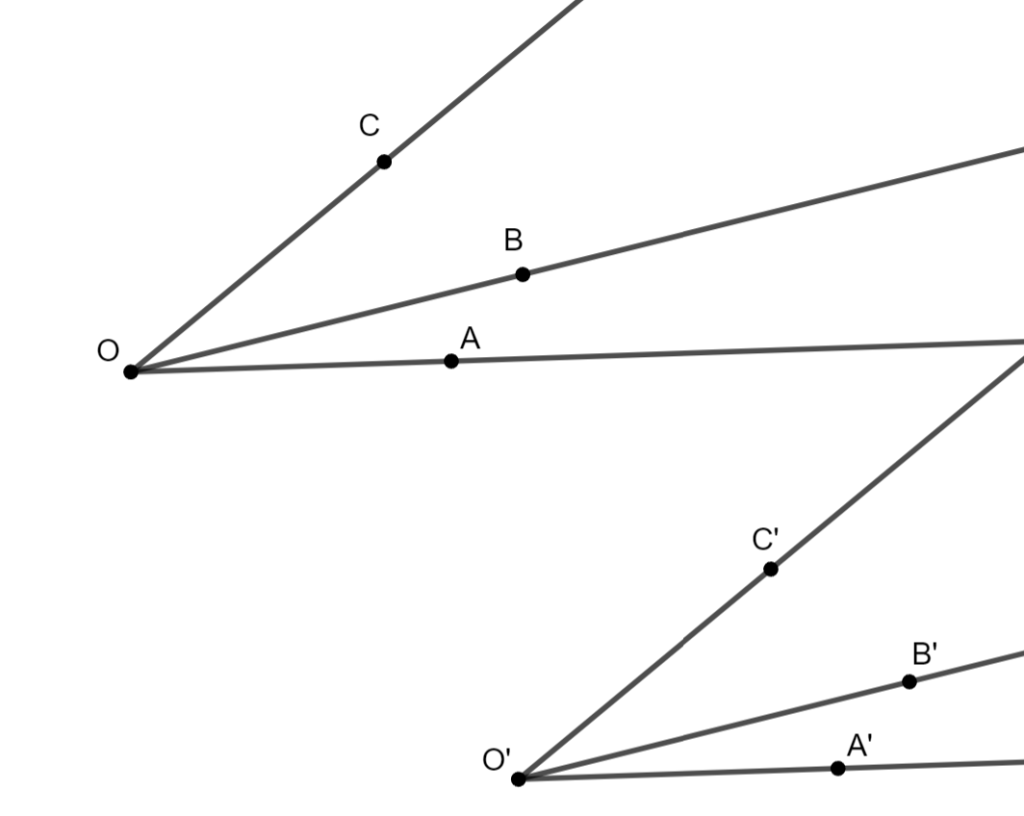
$\angle \alpha \cong \angle \beta \text{ y } \angle \beta \cong \angle \gamma \implies \angle \alpha \cong \angle \gamma$

Axioma III.6 (Suma de ángulos)

Si ∠AOB ≅ ∠A′O′B′ y ∠BOC ≅ ∠B′O′C′,

y las semirrectas OB y O′B′ están en el interior de ∠AOC y ∠A′O′C′ respectivamente, entonces:

$\angle AOC \cong \angle A'O'C'$

Congruencia de Triángulos

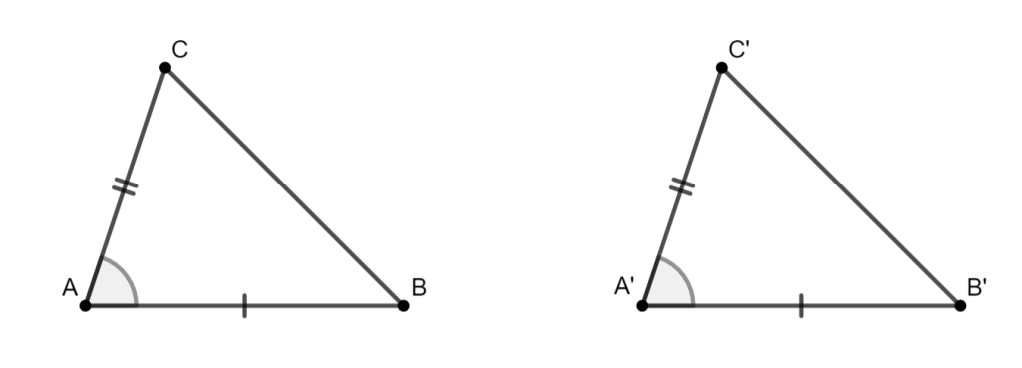
Axioma III.7

Si en dos triángulos △ABC y △A′B′C′ se cumple:

$\overline{AB}\cong \overline{A'B'}$

$\angle{A}\cong \angle{A'}$

$\overline{AC}\cong \overline{A'C'}$

Entonces:

$\triangle ABC \cong \triangle A'B'C'$

Mate

Roberto Rodriguez