Un ángulo se define como una figura geométrica específica formada por la unión de dos semirrectas (o rayos) que comparten un origen común pero no son colineales. Aquí presentamos la definición rigurosa, sus componentes clave y su base en los axiomas:
Definición Formal
Dados tres puntos no alineados A, O, B, el ángulo ∠AOB es la unión de:
- La semirrecta OA.
- La semirrecta OB.
En símbolos:

Elementos:
- Vértice: Punto O (origen común de las semirrectas).
- Lados: Semirrectas OA y OB.

Base en los Axiomas de Hilbert
Axiomas de Incidencia (Grupo I):
- Garantizan la existencia de las semirrectas OA y OB.
Axiomas de Orden (Grupo II):
- La no colinealidad de A, O, B implica que las semirrectas OA y OB no son semirrectas opuestas.
Axioma de Pasch (II5):
- Permite definir el interior del ángulo (región convexa entre los lados).
Casos Especiales
Ángulo llano:
- Si A, O, B son colineales con O entre A y B, el ángulo es una recta completa (no cumple la definición estándar).
Ángulo nulo:
- Si A = B u O-A-B (semirrectas coincidentes), el ángulo degenera a una única semirrecta.

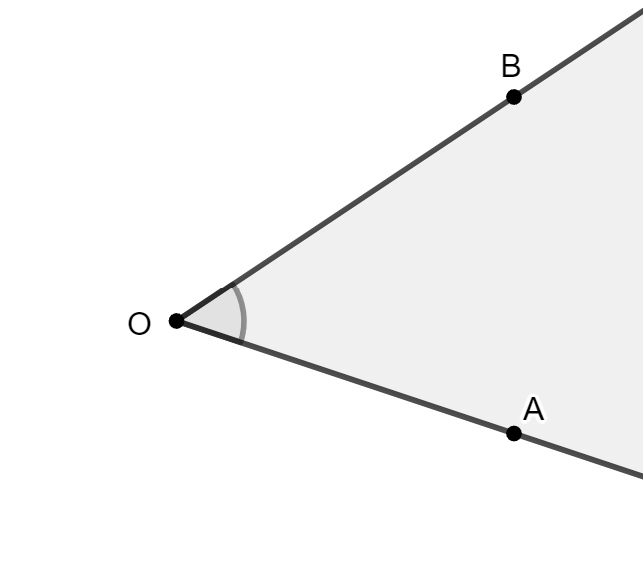
Interior y Exterior de un Ángulo
Interior:
- Conjunto de puntos P tales que:
- P está en el mismo semiplano que B respecto a la recta OA.
- P está en el mismo semiplano que A respecto a la recta OB.
Exterior:
- Puntos que no están en el interior ni en los lados del ángulo.
Importancia de la Definición
- Congruencia: Permite comparar ángulos usando movimientos rígidos (axiomas de congruencia de Hilbert).
- Polígonos: Los triángulos y otros polígonos se definen mediante ángulos y segmentos.
- Teoremas clave: Como el Teorema del Ángulo Exterior (en un triángulo, un ángulo exterior es mayor que los interiores no adyacentes).
Relación con la Convexidad
- Convexidad del interior: Si P y Q están en el interior de ∠AOB, entonces el segmento PQ también está en el interior.
- Demostración: Usa el Axioma de Pasch y la definición de semiplanos.
Ejemplo de Aplicación
Problema: Demostrar que si P está en el interior de ∠AOB, entonces la semirrecta OP también está en el interior.
Demostración:
- P está en el mismo semiplano que B respecto a la recta OA.
- Todo punto Q en la semirrecta OP cumple O-P-Q o O-Q-P, manteniendo la condición de semiplano.
La definición de ángulo como unión de semirrectas es minimalista pero poderosa, permitiendo construir resultados complejos sin apelar a nociones métricas (como grados). Es la base para:
- Geometría sintética: Demostraciones sobre congruencia y paralelismo.
- Extensiones: Geometrías no euclidianas, donde los axiomas de orden e incidencia aún aplican.






Deja un comentario