Mate

---

En el sistema axiomático de Hilbert, una semirrecta se define a partir de los axiomas de orden y el concepto primitivo «estar entre» (A-B-C).

---

Definición Formal

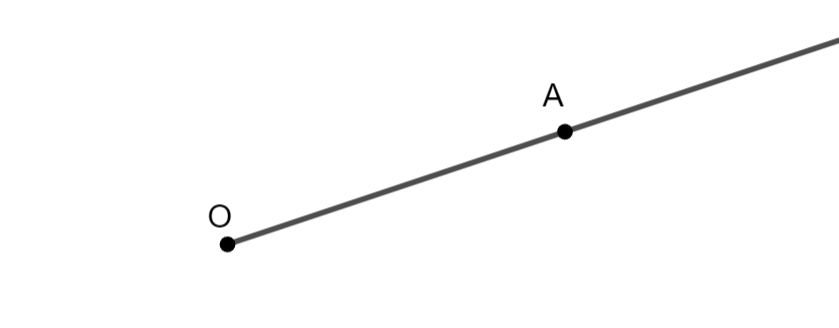
Dados dos puntos distintos O (origen) y A, la semirrecta de origen O que pasa por A es el conjunto de puntos formado por:

1. El origen O.
2. El punto A.
3. Todos los puntos P tales que:

• P está entre O y A (O-P-A), o
• A está entre O y P (O-A-P).

En símbolos:

---

Base en los Axiomas de Orden

Axioma II2 (Existencia de puntos intermedios):

• Garantiza que hay infinitos puntos P tales que O-A-P (extensión infinita de la semirrecta).

Axioma II3 (Unicidad del orden):

• Asegura que los puntos en la semirrecta están totalmente ordenados.

---

Propiedades Clave

1. Origen único: O es el único punto que no está «entre» otros dos puntos de la semirrecta.
2. Dirección: La semirrecta se extiende infinitamente desde O hacia A y más allá.
3. Convexidad: Si
   

---

Semirrectas opuestas

• Si A – O – B, entonces:
  • 
  • 
• Las semirrectas OA y OB reciben el nombre de semirrectas opuestas.

---

Relación con Otras Definiciones

• Segmento ( \overline{AB} ):
  • 
  • 

---

Importancia en la Geometría

1. Definición de ángulos: Un ángulo es la unión de dos semirrectas con el mismo origen.
2. Teoremas de separación: Las semirrectas permiten dividir la recta en regiones.
3. Congruencia: Para comparar ángulos, primero se necesitan semirrectas bien definidas.

---

La semirrecta es una figura geométrica fundamental que extiende el concepto de segmento hacia el infinito. Su definición precisa en Hilbert depende críticamente de:

1. La relación «estar entre».
2. Los axiomas de orden para garantizar su estructura infinita y convexa.

---