En el sistema axiomático de Hilbert, un semiplano es una de las dos regiones convexas en las que una recta divide a un plano. Su definición precisa se basa en los axiomas de orden y el Teorema de Separación del Plano. Aquí está la construcción rigurosa.
Definición Formal
Dada una recta r en un plano α, y un punto P ∈ α que no está en la recta r,
el semiplano de borde r que pasa por P es el conjunto:
- Otro semiplano:
Notación:
- Los dos semiplanos generados por r reciben el nombre de semiplanos opuestos.
Base en los Axiomas
Axioma de Incidencia I7:
- Si dos puntos están en un plano, la recta que los une está contenida en el plano.
Axioma de Orden II5 (Pasch):
- Garantiza que si una recta entra en un triángulo por un lado, debe salir por otro. Esto asegura que los semiplanos son convexos y disjuntos.
Propiedades Clave
Convexidad:
- Si A, B ∈ α_P, entonces el segmento AB ⊂ α_P.
- Demostración: Si existiera C ∈ segmento AB con C sin pertenecer al semiplano, entonces
contradiciendo el Axioma de Pasch aplicado a △PAB.

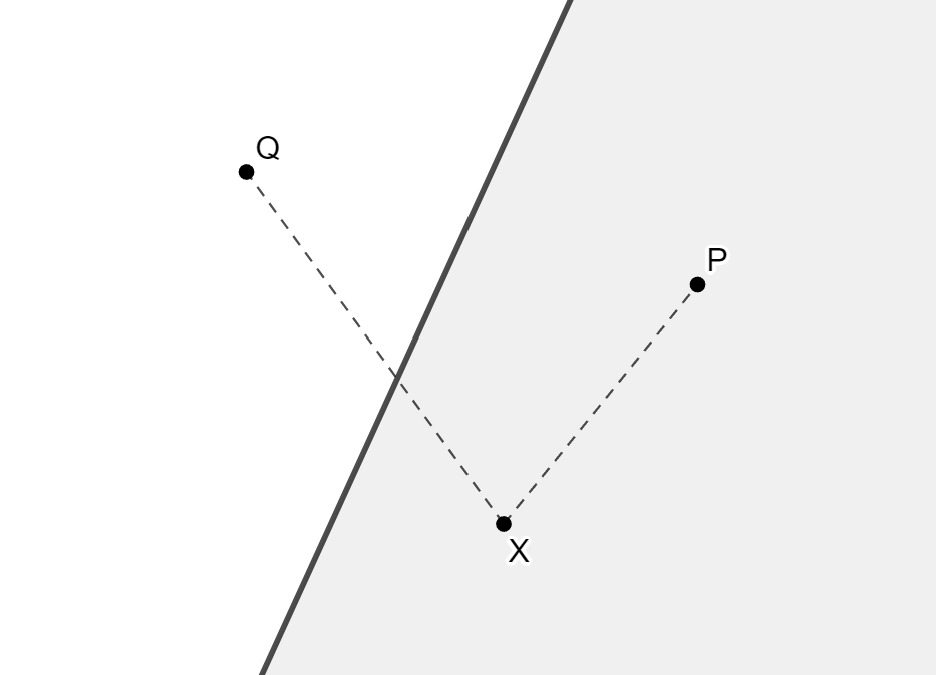
Separación:
- Si A ∈ α_P y B ∈ α_Q, entonces
.
Disjunción:
(solo comparten la recta r, borde de los semiplanos).
Ejemplo Visual
Relación con el Teorema de Separación del Plano
Esta definición es una aplicación directa del teorema, que demuestra que:
- Todo plano se divide en dos semiplanos convexos.
- La recta r es la frontera común.
Aplicaciones
- Definir ángulos: Un ángulo es la intersección de dos semiplanos.
- Polígonos convexos: Son intersecciones de semiplanos.
- Geometría proyectiva: Extiende estos conceptos al añadir «puntos al infinito».
Un semiplano es una región convexa del plano limitada por una recta, cuya definición depende críticamente de:
- La relación «estar entre» (orden).
- El Axioma de Pasch para garantizar convexidad.






Deja un comentario