Fórmula de la distancia entre dos puntos en el plano

Para calcular la distancia entre dos puntos (A(x_1, y_1)) y (B(x_2, y_2)) en el sistema cartesiano, usamos el Teorema de Pitágoras, ya que la distancia forma la hipotenusa de un triángulo rectángulo imaginario.

Fórmula

$\boxed{d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}}$

Donde:

d = distancia entre los puntos.
(x_1, y_1) = coordenadas del primer punto.
(x_2, y_2) = coordenadas del segundo punto.

Paso a paso

Identifica las coordenadas de ambos puntos.

Ejemplo: A (1, 2) y B (4, 6).

Calcula las diferencias en los ejes (X) e (Y):

$\Delta x = x_2 - x_1 = 4 - 1 = 3$
$\Delta y = y_2 - y_1 = 6 - 2 = 4$

Eleva al cuadrado ambas diferencias:

$(\Delta x)^2 = 3^2 = 9$
$(\Delta y)^2 = 4^2 = 16$

Suma los cuadrados:

9 + 16 = 25.

Saca la raíz cuadrada:

$d = \sqrt{25} = 5$

¡La distancia entre A y B es 5 unidades!

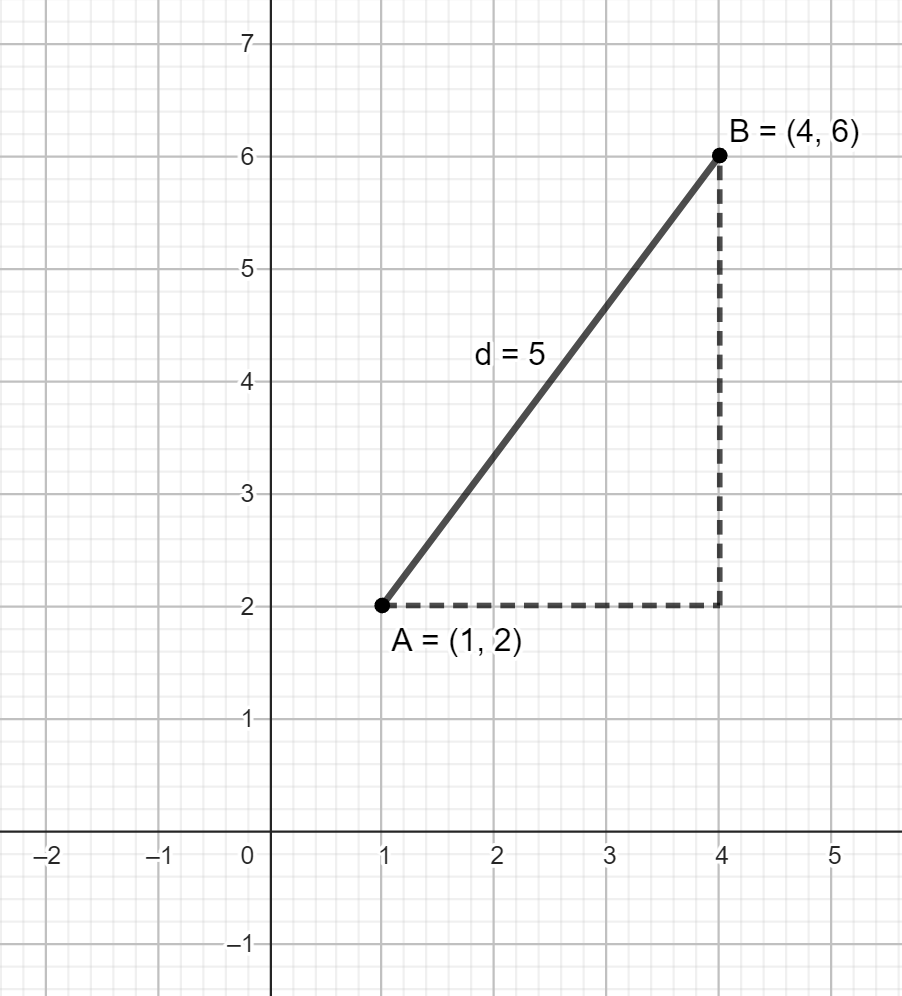
Demostración gráfica

Imagina un triángulo rectángulo donde:

El cateto horizontal mide
$\Delta x = 3$
El cateto vertical mide
$\Delta y = 4$
La hipotenusa es la distancia d = 5 (clásico triángulo 3-4-5).

Casos especiales

Misma abscisa
$(x_1 = x_2)$

La distancia es la diferencia en (Y):
$d = |y_2 - y_1|$
Ejemplo: Entre (3, 1) y (3, 5) → d = 4.

Misma ordenada
$(y_1 = y_2)$

La distancia es la diferencia en (X):
$d = |x_2 - x_1|$
Ejemplo: Entre (-2, 4) y (3, 4) → d = 5.

Ejercicios para practicar

Calcula la distancia entre (0, 0) y (3, 4).
Solución: (d = 5) (¡triángulo 3-4-5 otra vez!).
Encuentra la distancia entre (-1, 5) y (2, 1).
Solución:
$d = \sqrt{(2 - (-1))^2 + (1 - 5)^2} = \sqrt{9 + 16} = 5$
Si la distancia entre (a, 3) y (5, 7) es 5, ¿cuánto vale a?
Pista: Resuelve
$\sqrt{(5 - a)^2 + 16} = 5$

Aplicaciones

Geometría: Calcular perímetros y áreas.
Física: Distancias en movimiento parabólico.
GPS: Distancia entre coordenadas reales.

Mate

Roberto Rodriguez