Mate

---

🌍 Introducción: El Axioma que Desafió a los Genios

«Durante más de 2,000 años, un único postulado de *Los Elementos* de Euclides (300 a.C.) atormentó a matemáticos: el Postulado de las Paralelas. Su complejidad generó dudas: ¿Era realmente un axioma o podía demostrarse? Los intentos por probarlo llevaron a algo inesperado: la creación de geometrías no euclidianas, donde los ángulos de un triángulo no suman 180° y las paralelas se cruzan. Esta es la historia de cómo un problema aparentemente simple revolucionó nuestra comprensión del espacio.»

---

El Postulado V: El «Escándalo» de Euclides

¿Qué dice el Postulado?

«Si una recta corta a otras dos formando ángulos internos menores a dos rectos, esas dos rectas prolongadas se cortan en el lado donde están los ángulos menores.»

En español claro:

• Imagina dos rectas y una transversal. Si los ángulos internos suman menos de 180°, las rectas no son paralelas y se cruzarán.

💡 ¿Por qué era polémico?

• Euclides lo usó para probar teoremas clave (como la suma de ángulos en triángulos), pero no era autoevidente como sus otros 4 postulados.

---

Los Intentos Fallidos por «Demostrarlo»

La Obsesión de los Matemáticos

Durante siglos, genios como Ptolomeo, Proclo y Saccheri intentaron probar el Postulado V a partir de los otros cuatro. Todos fracasaron.

El Engaño de Saccheri (1733)

• Girolamo Saccheri creyó haberlo demostrado por contradicción, pero en realidad descubrió propiedades de geometrías no euclidianas… ¡y las descartó por «absurdas»!

Frase célebre: «Dios castiga con locura a quien se atreve a negar el Postulado V» (Saccheri, antes de crear sin querer una geometría alternativa).

---

La Revolución: Lobachevsky y Bolyai

Geometría Hiperbólica (1829–1832)

• Nikolai Lobachevsky y János Bolyai (por separado) probaron que el Postulado V era independiente: podía negarse sin contradicción.
• Nueva regla: «Por un punto exterior a una recta, pasan infinitas paralelas.»

Consecuencias:

• Triángulos con suma de ángulos < 180°.
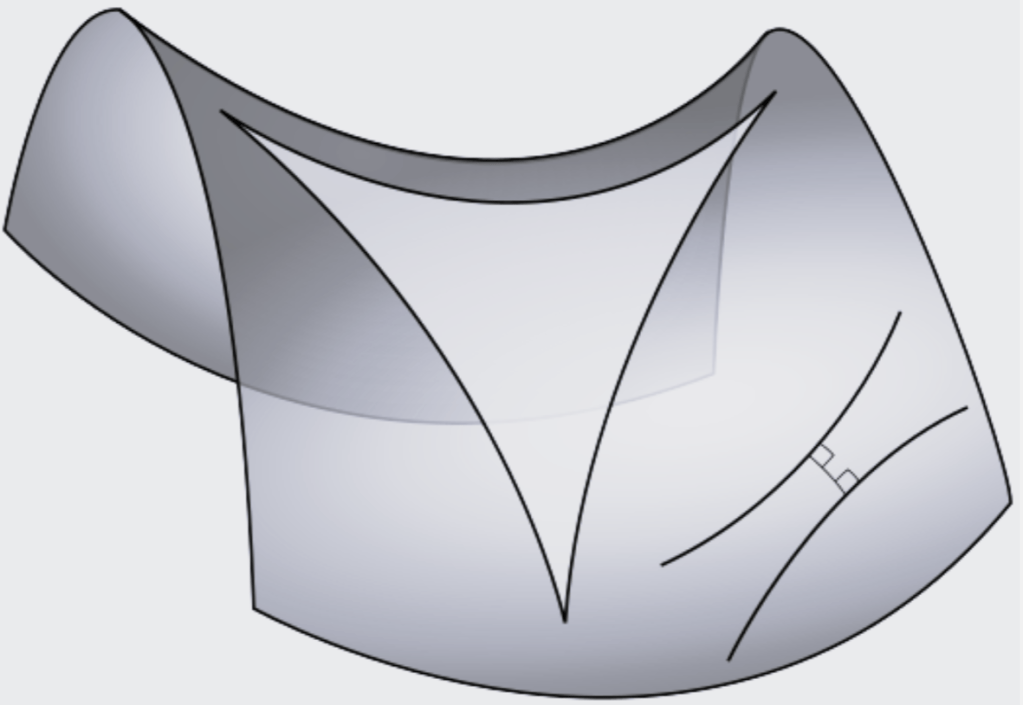
• Curvatura negativa (como una silla de montar).

La Venganza de Gauss

• Carl Friedrich Gauss ya lo sospechaba, pero no lo publicó por miedo al escándalo («El grito de los beocios», decía).

---

Riemann y la Geometría Elíptica (1854)

¿Y si no hay paralelas?

• Bernhard Riemann propuso una geometría donde no existen paralelas (todas las rectas se cortan).
• Nuevo mundo:
• Triángulos con suma de ángulos > 180° (como en una esfera).
• Curvatura positiva (ej: la Tierra).

Ejemplo práctico:

• En un globo terráqueo, dos meridianos son «rectas» que se cruzan en los polos.

---

Un Problema para Experimentar

Desafío: «Dibuja un triángulo en una esfera (usando arcos de círculos máximos) y mide sus ángulos. ¿Cuánto suman?»

Solución:

• Ejemplo: Un triángulo entre el Ecuador, un meridiano y otro meridiano a 90°.
• Ángulos: 90° + 90° + 90° = 270°.

---

El Legado: De Euclides a Einstein

Impacto en la Ciencia Moderna

• Relatividad General (1915): Einstein usó geometría no euclidiana para describir la gravedad como curvatura del espacio-tiempo.
• Cosmología: El universo podría ser cerrado (elíptico), abierto (hiperbólico) o plano (euclidiano).

Frase final: «Euclides pensó que estaba definiendo el espacio, pero en realidad estaba abriendo una puerta a infinitos universos matemáticos.»

---

📌 Bonus Track

• Debate: «¿Es la geometría euclidiana una ‘verdad absoluta’ o solo un caso particular?»
• Actividad: Usar GeoGebra para explorar triángulos en superficies curvas.
• Analogía: Comparar las geometrías con mundos de videojuegos (ej: Minecraft euclidiano vs. HyperRogue hiperbólico).

🌌📐 ¿Quieres profundizar? Podemos añadir:

• Cómo Poincaré visualizó el plano hiperbólico con su disco.
• Una biografía cómic de Lobachevsky (el «Copérnico de la geometría»).

---