Los axiomas formalizan la noción de «estar entre», permitiendo definir conceptos como segmento, rayo, y polígonos, así como establecer propiedades de ordenamiento geométrico.
Relación primitiva: «Entre»
- Relación ternaria: Dados tres puntos A, B, C alineados, se dice que B está entre A y C (notación: A-B-C).
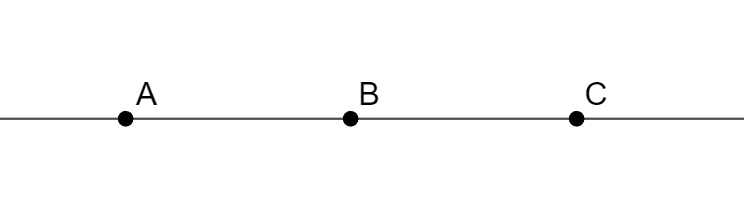
- Propiedad: Ordena los puntos alineados
En la geometría de Hilbert, los axiomas de orden se basan en una única relación primitiva implícita: la relación ternaria «estar entre» (betweenness en inglés), denotada como A-B-C (que significa «el punto B está entre A y C»). Esta relación es suficiente para definir todas las demás nociones de orden (como «estar antes» o «después») sin necesidad de introducir nuevas relaciones primitivas. Aquí está el desglose detallado:
¿Por qué no se necesitan «estar antes» o «estar después»?
Hilbert evita relaciones binarias como «( A < B )» porque:
- La geometría es sintética: No depende de coordenadas ni de un sistema numérico externo.
- El orden es relativo:
- «Antes» o «después» dependen de la dirección elegida en la recta.
- La relación ( A-B-C ) es invariante bajo reversión (por el Axioma II1).
Cómo se definen «antes» y «después» a partir de «entre»
Aunque no son primitivas, estas nociones pueden derivarse:
- «( A ) está antes que ( B ) en la dirección de ( \overrightarrow{PQ} )»:
- Existe un punto ( C ) tal que ( P-Q-C ) y ( A-B-C ).
- Semirrectas:
- ( \overrightarrow{AB} ) incluye todos los puntos ( P ) tales que ( A-B-P ) o ( A-P-B ).
Ejemplo de Derivación
Objetivo: Ordenar los puntos ( A, B, C ) colineales.
Por el Axioma II3, solo una de estas es cierta:
- A-B-C (B está entre A y C).
- A-C-B (C esta entre A y B).
- B-A-C (A está entre B y C).
Orden lineal:
- Si A-B-C, el orden es (A, B, C) o (C, B, A) (dependiendo de la dirección elegida).
Relación con Otros Sistemas
- Geometría analítica:
- «Estar entre» se traduce a coordenadas: B está entre A y C si
B = tA + (1-t)C con t ∈ (0,1).
- «Estar entre» se traduce a coordenadas: B está entre A y C si
Importancia de la Minimalidad
Hilbert busca un sistema con el mínimo número de primitivos. Al usar solo «estar entre»:
- Evita redundancias.
- Mantiene la generalidad (funciona en cualquier geometría ordenada, no necesariamente euclidiana).
En la geometría de Hilbert, la única relación primitiva de orden es «estar entre» (( A-B-C )). Conceptos como «antes» o «después» son derivados y dependen del contexto (ej: elección de una semirrecta de referencia). Esta elección refleja el enfoque sintético y axiomático de Hilbert, donde la simplicidad y la autosuficiencia lógica son prioritarias.






Deja un comentario