¿Qué es una función?

Funciones

Definición de función

Definición formal:
Una función f es una relación entre dos conjuntos A (llamado dominio) y B (llamado codominio), que asigna a cada elemento x ∈ A un único elemento y ∈ B.

Se denota:
$f: A \to B \quad \text{ tal que } \quad x \mapsto y = f(x).$

Dominio (Dom f): Conjunto de todos los valores x para los cuales f(x) está definida.
Codominio: Conjunto B que contiene los posibles valores de salida.
Imagen (Im f): Subconjunto de B formado por los valores f(x) para cada x ∈ A.

Ejemplo 1:
La función
$f: \mathbb{R} \to \mathbb{R}$
definida por f(x) = x^2 tiene:

Dominio: R (todos los números reales).
Codominio: R.
Imagen:
$[0, +\infty) ) (porque ( x^2 \geq 0 )$

Representaciones de una función

Algebraica: Fórmula explícita (ej. f(x) = sen(x)).

Gráfica: Puntos (x, f(x)) en el plano cartesiano.

Importante: Verificar el test de la recta vertical: Una curva es función si toda recta vertical la corta en un solo punto.

Tabular: Valores discretos (ej. tabla de datos).

Ejemplo 2:
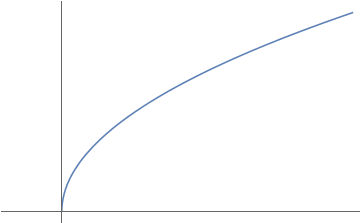
La función g(x) = √(x) está definida solo para x ≥ 0. Su gráfica es la mitad superior de una parábola horizontal.

Mate

Roberto Rodriguez