Definiremos en principio figura, figura convexa y figura cóncava para proporcionar un marco general y luego introducir conceptos específicos como segmentos, triángulos o polígonos. Aquí está la formalización rigurosa, alineada con el sistema de Hilbert y adaptada a un enfoque pedagógico claro:
Definición de Figura
En la geometría axiomática de Hilbert, una figura es:
- Cualquier conjunto de puntos en el plano o el espacio.
Ejemplos:
- Un punto aislado, un segmento, un conjunto de puntos alineados, un triángulo, un círculo.
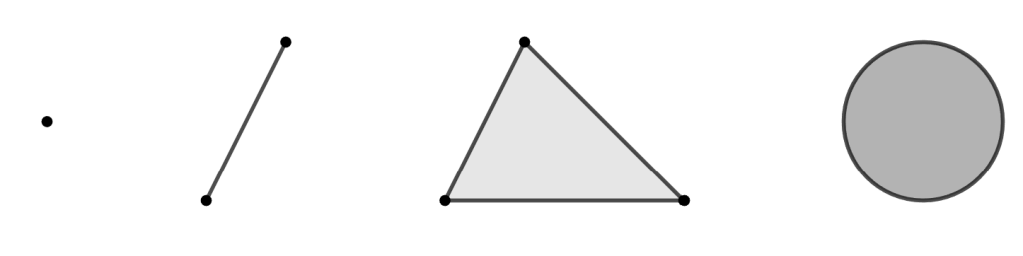
Base axiomática:
- No requiere axiomas adicionales; se apoya en los conceptos primitivos de punto, recta y plano.
Figura Convexa
Definición:
Una figura F es convexa si para todo par de puntos A, B ∈ F, el segmento AB está completamente contenido en F.
Ejemplos:
- Un segmento, un semiplano, el interior de un círculo.
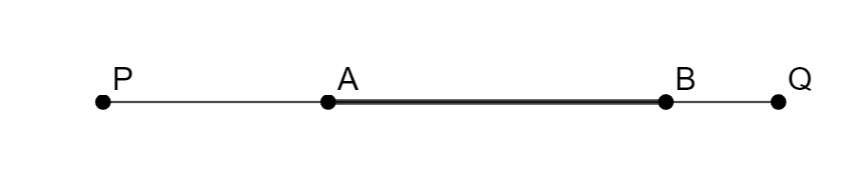

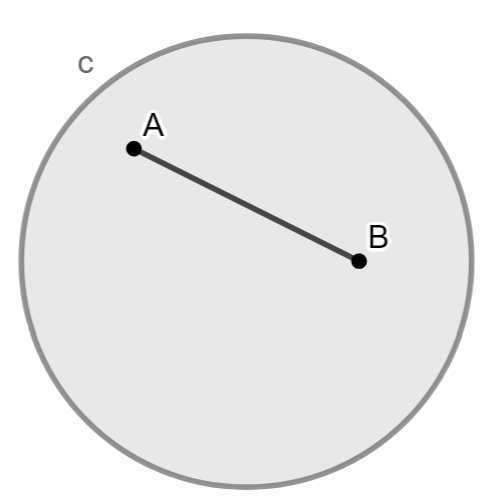
Teorema útil:
- La intersección de figuras convexas es convexa (demostrable con el Axioma de Pasch).
La convexidad es propiedad derivada de los axiomas de orden:
- La convexidad depende de la relación «estar entre» para definir segmentos.
Figura Cóncava (No Convexa)
Definición:
Una figura F es cóncava si existe al menos un par de puntos A, B ∈ F tal que:
Características:
- Tiene al menos un «entrante» o «hueco».
- Ejemplos: Una región en forma de «C», un polígono con un ángulo interno mayor a 180°.
Ejemplos
- El exterior de un ángulo agudo.

Relación con los axiomas:
- La concavidad se identifica al violar la definición de convexidad, usando el concepto de segmento.
Jerarquía de Definiciones
- Figura (conjunto de puntos).
- Segmento (figura convexa básica, definida con «estar entre»).
- Semirrecta y semiplano (figuras convexas derivadas).
- Polígonos (convexos o cóncavos, según sus ángulos).
Importancia en el Sistema de Hilbert
- Convexidad:
- El Axioma de Pasch (II5) implica que el interior de un triángulo es convexo.
- Aplicaciones:
- Permite demostrar teoremas sobre separación (ej: una recta divide al plano en dos semiplanos convexos).
Definir figura, convexidad y concavidad antes de segmentos o ángulos enriquece la comprensión estructural de la geometría. Estas nociones son la base para:
- Construir objetos más complejos (polígonos, poliedros).
- Demostrar propiedades topológicas (separación, conexidad).






Deja un comentario