Los axiomas formalizan la noción de «estar entre», permitiendo definir conceptos como segmento, rayo, y polígonos, así como establecer propiedades de ordenamiento geométrico.
Relación primitiva: «Entre»
- Relación ternaria: Dados tres puntos A, B, C alineados, se dice que B está entre A y C (notación: A-B-C).
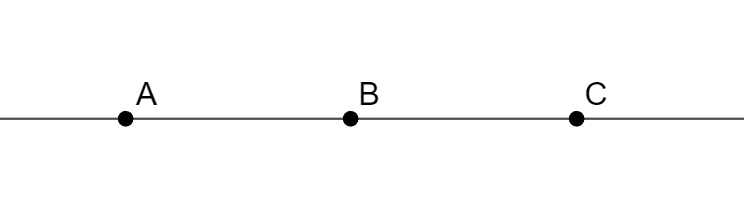
- Propiedad: Ordena los puntos alineados
Axioma II1 (Propiedad Simétrica)
- Si B está entre A y C, entonces B está entre C y A.
- Interpretación: El orden «entre» es indiferente a la dirección de la recta.
Axioma II2 (Existencia de un punto intermedio)
- Dados dos puntos distintos A y B, existe al menos un punto C tal que A – C – B.

- Corolario: Entre dos puntos existen infinitos punto.
Axioma II3 (Extensión de la recta)
- Dado dos puntos A y B, existe al menos un punto C tal que A – B – C.

Axioma II4 (Unicidad del orden)
- De tres puntos alineados distintos, solo uno puede estar entre los otros dos.
Axioma II5 (Axioma de Pasch)
- Si una recta r interseca a un triángulo △ABC cortando a un lado AB, entonces debe intersecar otro lado AC o BC.
- Formalización:
Dado △ABC y una recta r que no pasa por A, B, ni C:
- Importancia: Garantiza la «conexidad» del plano.





Deja un comentario