Mate

Demostración (paso a paso):

Datos iniciales:

• Sea AB la recta dada y C el punto exterior.

Construcción auxiliar:

• Se traza un segmento CD desde C hasta cualquier punto D en AB (Postulado 1).
• Se construye el ángulo ∠ DCE sobre CD igual al ángulo ∠ CDB (usando la Proposición 23, que permite copiar un ángulo en un punto dado).

Paralelismo garantizado:

• Los ángulos ∠ DCE y∠ CDB son alternos internos e iguales por construcción.
• Por la Proposición 27 (que establece que, si los ángulos alternos son iguales, las rectas son paralelas), la recta CE es paralela a AB.

---

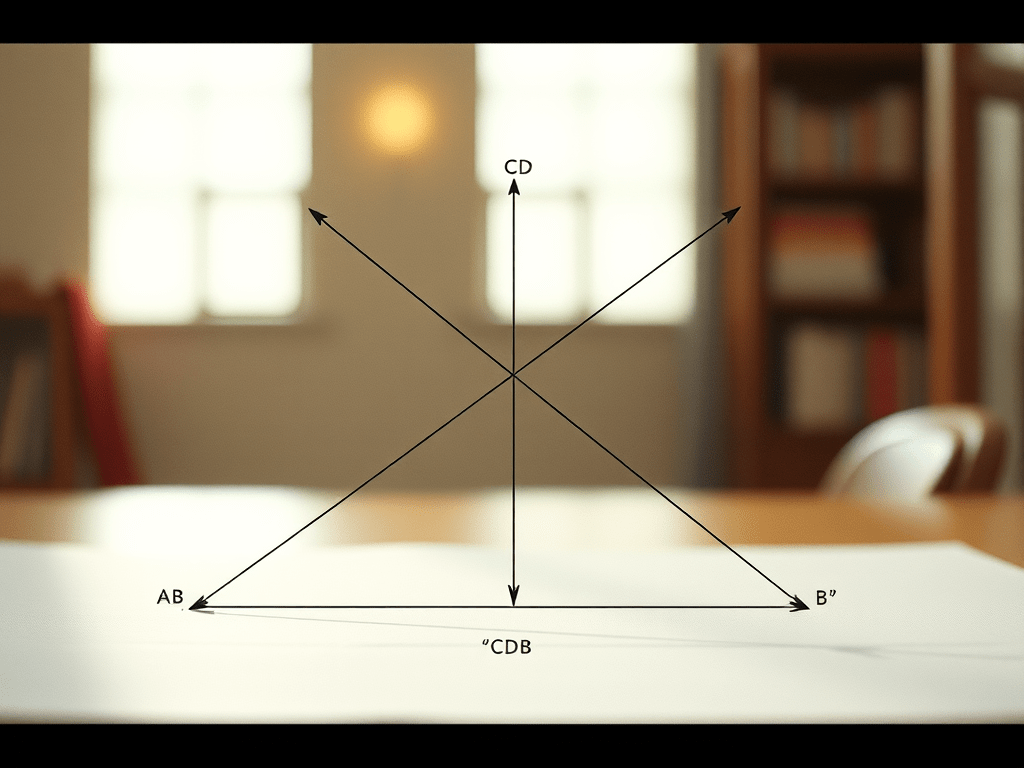
Visualización:

• AB es la recta dada.
• CD es el segmento auxiliar.
• ∠ DCE = ∠ CDB (ángulos alternos iguales).
• CE ∥ AB.

---

Importancia:

Herramienta fundamental:

• Esta construcción es clave para trabajar con paralelas en problemas geométricos, como la división de áreas (Libro VI) o el Teorema de Tales.

Uso del Postulado de las Paralelas:

• Aunque Euclides no usa explícitamente el 5º Postulado aquí, esta proposición depende indirectamente de él (en la Proposición 29, donde se prueba la recíproca).

Método generalizable:

• La técnica de copiar ángulos para garantizar paralelismo se aplica en construcciones más complejas, como polígonos regulares.

---

Ejemplo práctico:

Objetivo: Trazar una paralela a la recta AB que pase por C.
Pasos:

1. Elige un punto D en AB y únelo con C.
2. Con un transportador, mide ∠ DCB.
3. Copia ese ángulo en C para formar ∠ DCE.
4. Extiende CE: ¡esta es la paralela buscada!

---

Relación con otras proposiciones:

• Prop. 23: Permite copiar el ángulo necesario.
• Prop. 27: Justifica el paralelismo mediante ángulos alternos.
• Prop. 29: Demuestra propiedades de rectas paralelas cortadas por una transversal (usa el 5º Postulado).

---