Relaciones entre Puntos y Rectas
Estos axiomas describen cómo los puntos y las rectas interactúan:
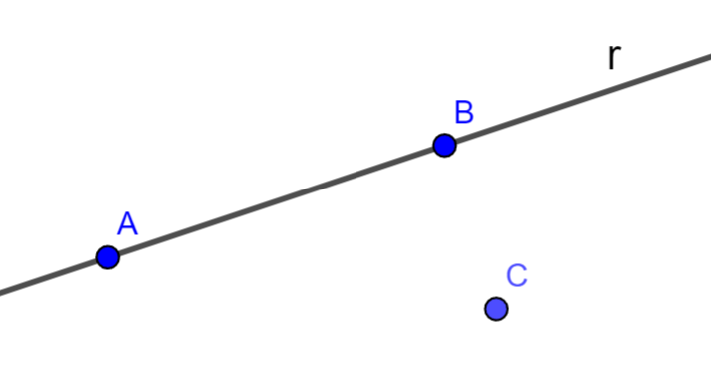
Axioma I1 (Unicidad de la recta):
Dados dos puntos distintos A y B, existe una única recta r que pasa por ambos.
- Notación:
- Implicación: Dos rectas distintas no pueden compartir más de un punto.

Axioma I2 (Existencia mínima):
Toda recta contiene al menos dos puntos.
- Propósito: Evita espacios triviales (ej. un solo punto).
Axioma I3 (Espacio Bidimensional):
Dada una recta existe al menos un punto que no pertenece a la recta.
- Existen al menos tres puntos no colineales (no todos en la misma recta).
- Propósito: Permite definir planos.
Relaciones entre Puntos y Planos
Estos axiomas vinculan puntos con planos:
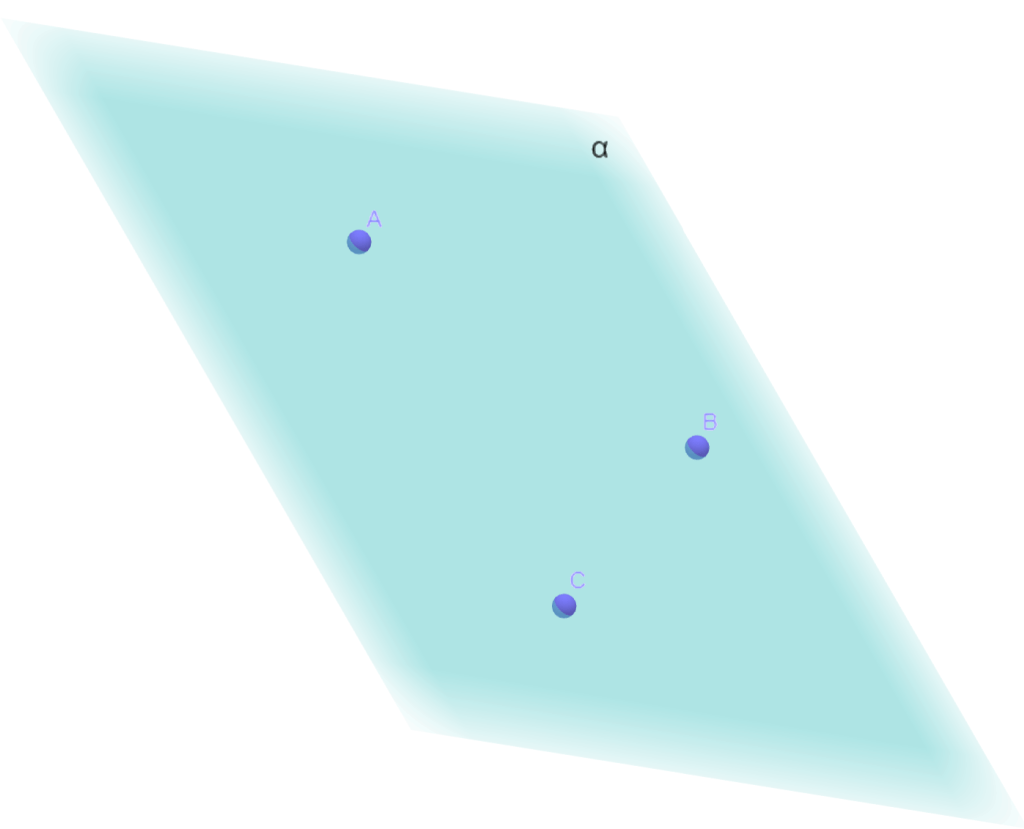
Axioma I4 (Determinación del plano):
Dados tres puntos no alineados A, B, C, existe un único plano α que los contiene.
- Notación: Los planos se nombran con letras griegas α, β, etc.
Axioma I5 (Puntos en el plano):
Todo plano contiene al menos tres puntos no alineados.
- Propósito: Evita espacios triviales (ej. una sola recta).
Axioma I6 (Existencia del espacio):
Dado un plano, existe al menos un punto que no pertenece a dicho plano.
- Existen al menos tres puntos no colineales (no todos en la misma recta).

Relaciones entre Puntos, Rectas y Planos
Axioma I7 (Recta incluida en un plano):
Si dos puntos A y B de una recta r están en un plano α, entonces toda la recta r está contenida en α.
- Corolario: Una recta está completamente determinada por dos de sus puntos en un plano.

Axioma I8 (Intersección de planos):
Si dos planos distintos α y β tienen al menos un punto en común, entonces su intersección es una recta.
- Implicación: Dos planos no pueden cortarse en solo un punto o en una curva.
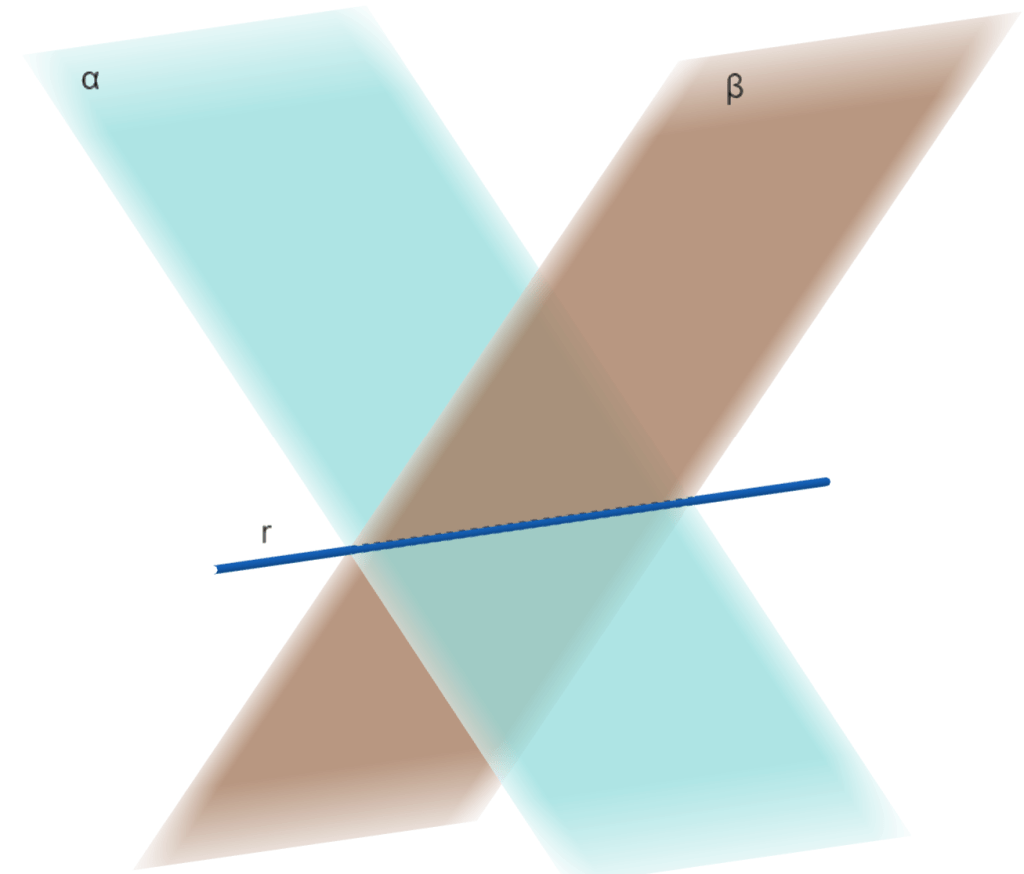






Deja un comentario