Definición de Puntos Coplanares
En geometría, los puntos coplanares son un conjunto de puntos que pertenecen al mismo plano. Es decir, existe un plano (superficie bidimensional infinita) que contiene a todos ellos.
Explicación Detallada
- Condición mínima:
- Tres puntos siempre son coplanares (porque tres puntos no colineales definen un único plano).
- Para cuatro o más puntos, no todos los conjuntos son coplanares. Ejemplo:
- Coplanares: Las esquinas de un cuadrado (4 puntos en un plano).
- No coplanares: Tres puntos en el suelo y uno en el aire (como los vértices de una pirámide triangular).
- Relación con otros conceptos:
- Si los puntos son coplanares, cualquier recta o segmento trazado entre ellos también estará en ese plano.
Cómo Determinar si Puntos son Coplanares
Método geométrico (para 4 puntos):
Verifica si 3 puntos son colineales:
- Si A, B y C están alineados, cualquier cuarto punto D estará en el mismo plano si pertenece a la recta o a una paralela.
Si no son colineales:
- Los puntos A, B, C definen un plano.
- El punto D es coplanar si satisface la ecuación del plano formado por A, B, C.
Aplicaciones
- Diseño gráfico: Verificar si objetos 3D están en una misma superficie.
- Arquitectura: Planos de construcción basados en puntos de referencia.
- Física: Análisis de fuerzas en un mismo plano (estática).
¿Puntos colineales vs. coplanares?
- Colineales: Todos en una misma recta (subconjunto de coplanares).
- Coplanares: Todos en un mismo plano, pero no necesariamente alineados.
Ejemplo visual:
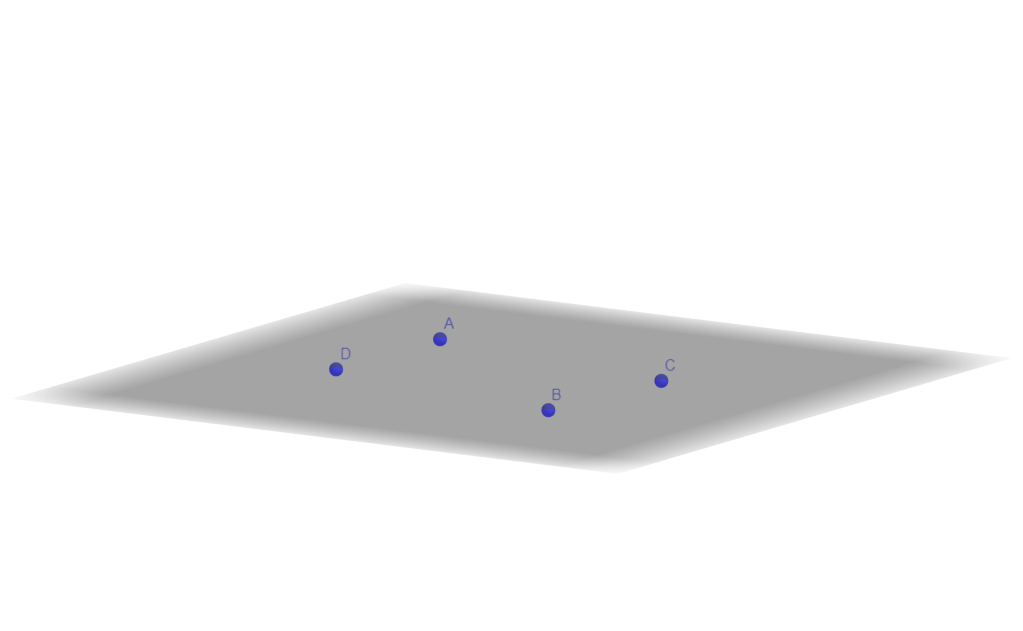

Los puntos coplanares son fundamentales en geometría euclidiana y aplicaciones prácticas. Su determinación depende de la dimensionalidad del espacio y puede verificarse mediante métodos geométricos o algebraicos.





Deja un comentario