Mate

Definición de Puntos Alineados

En la geometría de Hilbert, la alineación de puntos se define estrictamente a partir de los axiomas de incidencia y el concepto primitivo de recta. Aquí está la formalización rigurosa:

---

Definición Formal

Un conjunto de puntos se dice alineado (o colineal) si existe una recta tal que todos los puntos pertenecen a ella:

Base en los Axiomas

Axioma I1 (Unicidad de la recta):

• Dos puntos distintos determinan una única recta. Por tanto, tres o más puntos son alineados si todos caen en la recta definida por cualquier par de ellos.
• Ejemplo: Si son alineados, entonces:
  

Axioma I2 (Existencia mínima):

• Toda recta contiene al menos dos puntos, pero existen al menos tres puntos no alineados en el espacio.

---

Casos Especiales

Tres puntos alineados:

• A, B, C son alineados si y solo si uno de ellos está entre los otros dos (usando axiomas de orden).
• Ejemplo:
  

Puntos no alineados:

• Si tres puntos no están en una misma recta se dice que están no alineados y definen un único plano (Axioma I4).

---

Verificación de Alineación

Para verificar si tres puntos A, B, C son alineados:

1. Construye la recta AB (existente y única por Axioma I1).
2. Comprueba si:
   

• Si sí, son alineados.
• Si no, son no alineados y definen un plano.

---

Ejemplo Gráfico

---

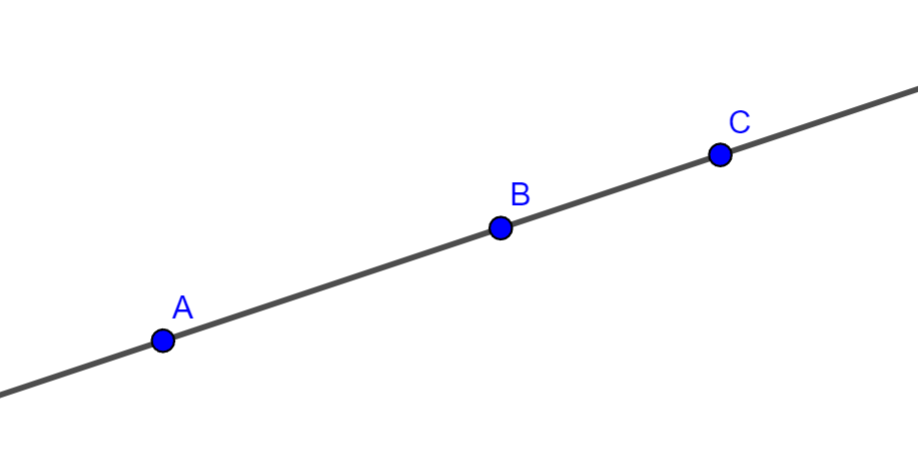
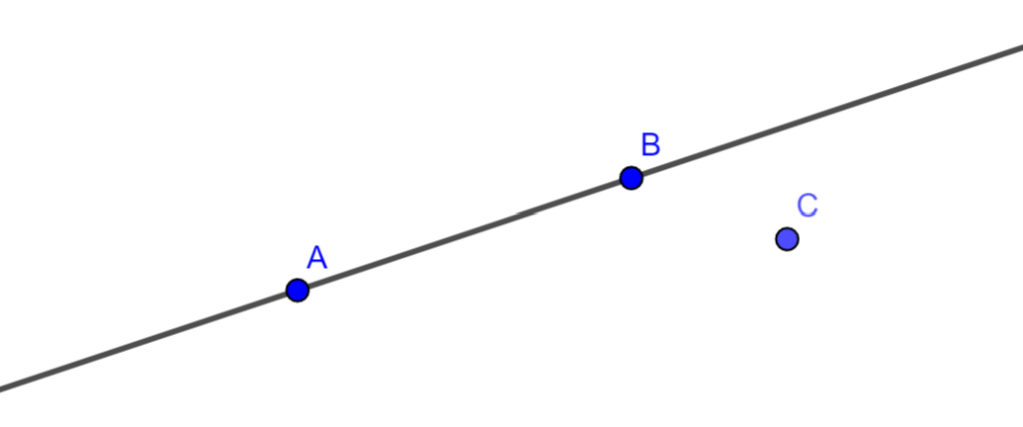
Relación con Axiomas de Orden

Si se incluyen los axiomas de orden, la alineación permite definir:

• Segmentos: el segmento AB es el conjunto de puntos alineados entre A y B.
• Semirrectas: la semirrecta de origen A que pasa por B incluye el segmento AB y todos los puntos alineados más allá de B.

---

La alineación es un concepto derivado de los axiomas de incidencia y orden, que caracteriza cuándo puntos comparten una misma recta. Es fundamental para definir figuras geométricas básicas (segmentos, ángulos) y avanzar hacia congruencia y continuidad.