Mate

La Geometría como Sistema Axiomático

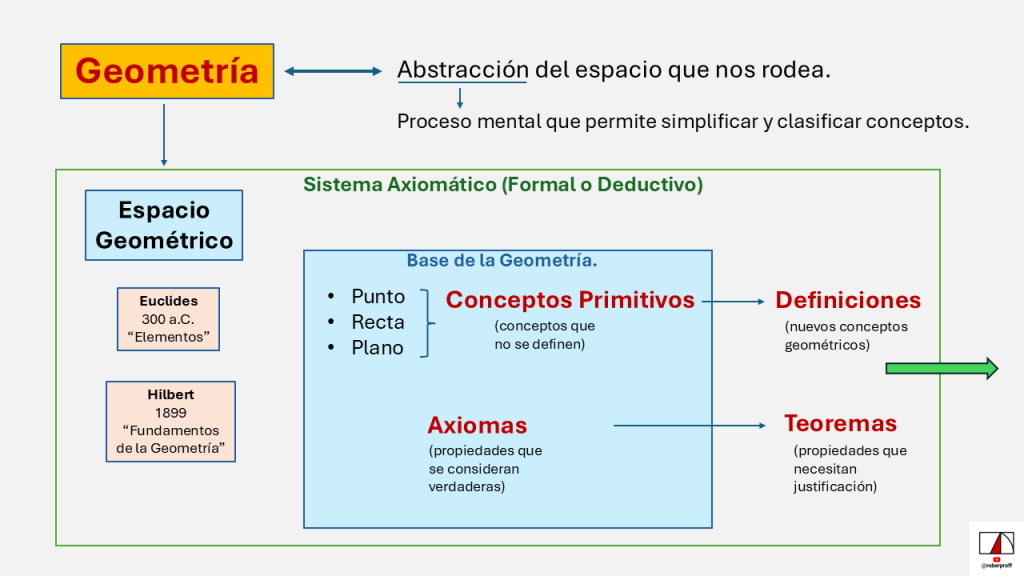
La geometría, en su enfoque moderno, es un sistema axiomático formal que organiza el conocimiento matemático a partir de conceptos primitivos, definiciones, axiomas y teoremas. A continuación, se detallan sus características y elementos clave, siguiendo el modelo establecido por David Hilbert en Fundamentos de la Geometría (1899).

Características Principales

Rigor lógico:

• Elimina ambigüedades de la geometría clásica (ej: Euclides definía punto como «lo que no tiene partes»).
• Usa conceptos no definidos (primitivos) y relaciones explícitas.

Independencia:

• Los axiomas no deben contradecirse ni derivarse de otros.
• Ejemplo: El quinto postulado de Euclides (de las paralelas) es independiente de los otros cuatro.

Completitud:

• Todos los teoremas deben demostrarse a partir de los axiomas.

Consistencia:

• No genera contradicciones lógicas. Hilbert probó la consistencia relativa de su sistema.

Elementos del Sistema Axiomático

A. Conceptos Primitivos

Términos no definidos, base de todas las definiciones posteriores. En Hilbert:

1. Punto (A, B, C…).
2. Recta (r, s, t…).
3. Plano (α, β, γ…).
4. Relaciones primitivas:

• Incidencia («pertenece a»).
• Entre (orden).
• Congruencia (equivalencia de segmentos/ángulos).

B. Axiomas

Proposiciones que se aceptan sin demostración. En Hilbert se agrupan en:

Axiomas de Incidencia:

• Ejemplo: Dos puntos determinan una única recta.

Axiomas de Orden:

• Ejemplo: De tres puntos alineados, uno está entre los otros dos.

Axiomas de Congruencia:

• Ejemplo: Segmentos congruentes pueden superponerse.

Axioma de las Paralelas (euclidiano):

• Por un punto exterior a una recta pasa una única paralela.

Axiomas de Continuidad:

• Incluyen el axioma de Arquímedes y el de completitud.

C. Definiciones

Conceptos derivados de los primitivos y axiomas. Ejemplos:

• Segmento: ( \overline{AB} = {A, B} \cup {P \mid A-P-B} ).
• Ángulo: Unión de dos semirrectas con origen común.
• Triángulo: Figura formada por tres segmentos que unen tres puntos no colineales.

D. Teoremas

Proposiciones demostradas a partir de axiomas y definiciones.

• Ejemplo: La suma de los ángulos de un triángulo es 180° (en geometría euclidiana).

Estructura Lógica

Conceptos Primitivos → Axiomas → Definiciones → Teoremas  

Ejemplo: Demostración de un Teorema

Teorema: Dos rectas distintas tienen a lo sumo un punto en común.

1. Axioma usado: Dos puntos determinan una única recta (Incidencia I1).
2. Demostración: Si dos rectas tuvieran dos puntos en común, serían la misma recta.

Tipos de Geometrías Axiomáticas

Geometría Euclidiana:

• Acepta el postulado de las paralelas. Válida en espacios planos.

Geometrías No Euclidianas:

• Hiperbólica: Infinitas paralelas (curvatura negativa).
• Elíptica: 0 paralelas (curvatura positiva, como en una esfera).

Geometría Proyectiva:

• Sin paralelas; todas las rectas se intersecan.

Importancia del Enfoque Axiomático

• Fundamentos de la Matemática: Precisa qué se asume y qué se demuestra.
• Aplicaciones: Desde física teórica (relatividad, que usa geometría no euclidiana) hasta gráficos computacionales.
• Pedagogía: Enseña a razonar deductivamente.

Bibliografía Recomendada

• Hilbert, D. (1899). Grundlagen der Geometrie (Fundamentos de la Geometría).
• Moise, E. (1963). Elementary Geometry from an Advanced Standpoint.

Este marco axiomático es la base para explorar desde la geometría escolar hasta teorías avanzadas.