El Plano es un Concepto Primitivo en Geometría Euclidiana
En la geometría clásica de Euclides, el plano es el tercer concepto primitivo fundamental, junto con el punto y la recta. Euclides lo define en el Libro I, Definición 5 como:
«Una superficie es aquello que solo tiene longitud y anchura»,
y más adelante especifica que un plano es una superficie que «yace por igual respecto de las rectas que están en él».
Características Esenciales
Como noción primitiva, el plano se entiende intuitivamente como:
- Bidimensional: Extensión infinita en longitud y anchura, pero sin grosor.
- Ilimitado: No tiene bordes ni fronteras.
- Determinado por tres puntos no colineales (o equivalentemente, por una recta y un punto exterior, o dos rectas que se cortan).
Representaciones y Notaciones
- Gráficamente:
Se dibuja como un paralelogramo (usualmente un rectángulo) para sugerir su extensión infinita, con líneas tenues en los bordes para indicar continuidad:
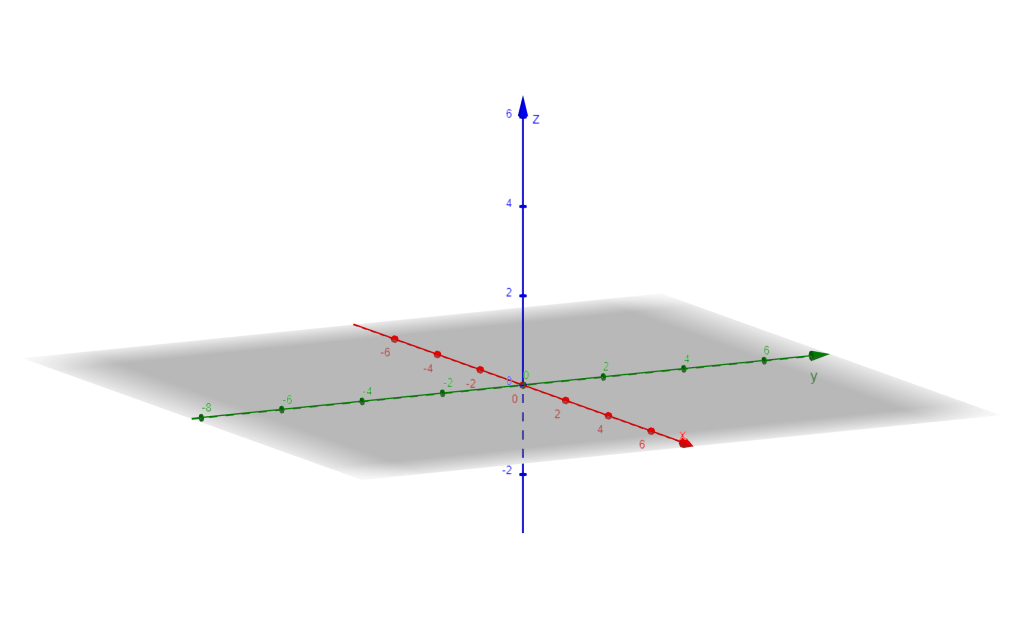
- Notación:
- Letras griegas (π, α, β).
- Tres puntos no alineados (plano ABC).
- En geometría analítica: ecuación general ( ax + by + cz + d = 0 ) (en ℝ³).
- Modelos físicos:
- Una hoja de papel (idealizada sin grosor).
- Una pantalla en 2D (ej: pizarra digital).
Usos en Construcciones Geométricas
El plano es el «escenario» donde se definen:
- Figuras planas: Triángulos, polígonos, círculos.
- Ángulos: Intersección de dos rectas en el plano.
- Transformaciones: Traslaciones, rotaciones, simetrías.
- Teoremas clásicos:
- Teorema de Pitágoras (relación en un plano rectángulo).
- Teorema de Desargues (sobre triángulos proyectivos).
Formalizaciones Modernas
En enfoques actuales, el plano se redefine con mayor rigor:
- Geometría analítica:
- En ℝ²: Conjunto de puntos ((x, y)) que satisfacen ecuaciones lineales.
- En ℝ³: Ecuación ( ax + by + cz = d ).
- Geometría vectorial:
- Plano como espacio generado por dos vectores linealmente independientes: ( \vec{r} = \vec{a} + t\vec{b} + s\vec{c} ).
- Topología:
- Espacio homeomorfo a ℝ² (ej: plano de Hausdorff).
Aplicaciones
- Arquitectura: Diseño de estructuras planas (muros, pisos).
- Física: Movimiento en 2D (tiro parabólico).
- Cartografía: Proyecciones de mapas (Mercator).
- Grágicos 3D: Planos de corte en modelos computacionales.
Comparación con Otras Superficies
| Concepto | Dimensión | Curvatura | Ejemplo |
|---|---|---|---|
| Plano | 2D | Cero (euclidiano) | Hoja de papel ideal |
| Esfera | 2D | Positiva | Superficie terrestre |
| Hiperboloide | 2D | Negativa | Silla de montar |
El plano euclidiano, aunque aparentemente simple, es la base de la geometría clásica y moderna. Desde su tratamiento intuitivo en Los Elementos hasta su formalización en álgebra y topología, sigue siendo esencial para entender desde problemas cotidianos hasta teorías físicas como la relatividad (donde el espacio-tiempo local es aproximadamente plano).






Deja un comentario